📘 अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन (Light – Reflection and Refraction)

✦ पाठ का सारांश (Chapter Summary)

यह अध्याय प्रकाश की दो प्रमुख घटनाओं, परावर्तन (Reflection) और अपवर्तन (Refraction) का अध्ययन कराता है। इसमें दर्पण व लेंस के सूत्र, चिह्न परिपाटी, आवर्धन, अपवर्तनांक तथा उनके दैनिक जीवन में उपयोग को समझाया गया है।

✦ विस्तृत नोट्स (Detailed Notes)

🔹 1. प्रकाश का परावर्तन (Reflection of Light)

परावर्तन के नियम
1. आपतन कोण (∠i) = परावर्तन कोण (∠r)।
2. आपतित किरण, परावर्तित किरण और अभिलंब एक ही तल में होते हैं।
समतल दर्पण में प्रतिबिंब
- प्रतिबिंब सदैव आभासी, सीधा और समान आकार का होता है।
- प्रतिबिंब दर्पण के पीछे वस्तु से समान दूरी पर बनता है।
- प्रतिबिंब पार्श्व उलटा (laterally inverted) होता है।

🔹 2. गोलीय दर्पण (Spherical Mirrors)

प्रकार
1. अवतल दर्पण (Concave Mirror) – परावर्तक सतह भीतर की ओर।
2. उत्तल दर्पण (Convex Mirror) – परावर्तक सतह बाहर की ओर।
मुख्य पद (Key Terms)
- ध्रुव (Pole – P): दर्पण का केंद्र।
- वक्रता केंद्र (C): उस गोले का केंद्र जिसका दर्पण भाग है।
- वक्रता त्रिज्या (R): P और C की दूरी।
- मुख्य अक्ष (Principal Axis): P और C से गुजरने वाली रेखा।
- मुख्य फोकस (F): समानांतर किरणें परावर्तित होकर जहाँ मिलती हैं (अवतल) या जहाँ से आती प्रतीत होती हैं (उत्तल)।
- फोकस दूरी (f): P और F के बीच की दूरी।
- संबंध: $f=R/2f = R/2$
दर्पण सूत्र (Mirror Formula):
$1/v+1/u= 1/f$
जहाँ $u=u =$ वस्तु दूरी, $v=v =$ प्रतिबिंब दूरी, $f=f =$ फोकस दूरी

चिह्न परिपाटी (Sign Convention for Mirrors)

दर्पण की ध्रुव से मुख्य अक्ष (Principal Axis) के साथ मापी गई दूरी ली जाती है।
दर्पण के सामने (Left side, वस्तु की ओर) की दूरी को ऋणात्मक (-ve) माना जाता है।
दर्पण के पीछे (Right side, प्रतिबिंब की ओर) की दूरी को धनात्मक (+ve) माना जाता है।

आवर्धन (Magnification):
$m=h′/ h=−v \ -u$
- $m> 0$ ⇒ आभासी, सीधा प्रतिबिंब
- $m< 0$ ⇒ वास्तविक, उल्टा प्रतिबिंब

🔹 3. प्रकाश का अपवर्तन (Refraction of Light)

परिभाषा: प्रकाश का एक माध्यम से दूसरे माध्यम में जाने पर अपने पथ को मोड़ लेना।
कारण: माध्यम बदलने से प्रकाश की चाल बदलती है।
अपवर्तन के नियम (Laws of Refraction / Snell’s Law)
1. आपतित किरण, अपवर्तित किरण और आपतन बिंदु पर खींचा गया अभिलंब — तीनों एक ही तल (plane) में होते हैं।
2. किन्हीं दो माध्यमों के लिए आपतन कोण (∠i) और अपवर्तन कोण (∠r) के sine का अनुपात एक नियतांक होता है।
$i\sin r =$
जहाँ,
- $i =$ आपतन कोण (Angle of Incidence)
- $r =$ अपवर्तन कोण (Angle of Refraction)
- $μ =$ अपवर्तनांक (Refractive Index)

🔹 4. अपवर्तनांक (Refractive Index)

सूत्र:
$n=c/v$
जहाँ $c=c =$ निर्वात में प्रकाश की चाल (3×10⁸ m/s), $v=v =$ माध्यम में प्रकाश की चाल
अधिक अपवर्तनांक ⇒ अधिक प्रकाशिक सघन माध्यम।
उदाहरण: वायु < जल < काँच < हीरा

🔹 5. लेंस (Lenses)

प्रकार:
- उत्तल लेंस (Convex) – बीच से मोटा, अभिसारी (converging)।
- अवतल लेंस (Concave) – बीच से पतला, अपसारी (diverging)।
लेंस सूत्र (Lens Formula):
$1/v-1/u=1/f$
आवर्धन:
$m=h'/h=v/u$
लेंस की क्षमता (Power of a Lens):
$P=1f(f in meters)P = \frac{1}{f} \quad (f \text{ in meters})$
- मात्रक: डाइऑप्टर (D)
- उत्तल लेंस ⇒ $+ve+ve$
- अवतल लेंस ⇒ $-ve-ve$

✦ CBSE परीक्षा के लिए महत्वपूर्ण बिंदु

चिह्न परिपाटी पर विशेष ध्यान दें।
दर्पण सूत्र व लेंस सूत्र के बीच का अंतर याद रखें।
आवर्धन के मान से प्रतिबिंब की प्रकृति जानना सीखें।
$f=R/2f = R/2$ का संबंध हमेशा याद रखें।
उपयोग से संबंधित प्रश्न जरूर आते हैं (अवतल दर्पण: हेडलाइट, उत्तल दर्पण: साइड मिरर)।
अपवर्तनांक और प्रकाशिक घनत्व का संबंध समझें।
लेंस की क्षमता (P = 1/f) और उसका मात्रक डाइऑप्टर याद रखें।
किरण आरेखों का अभ्यास करें।

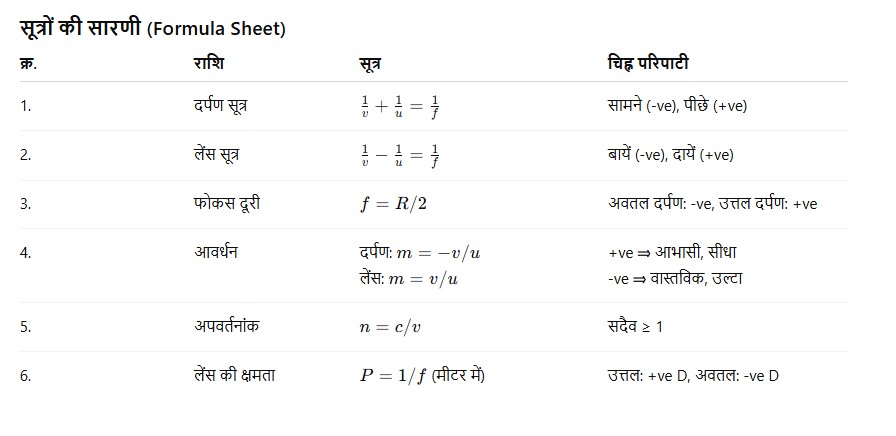
✦ सूत्रों की सारणी (Formula Sheet)

क्रम	सूत्र	विवरण
1	$1/v+1/u=1/f$	दर्पण सूत्र
2	$1/v-1/u=1/f$	लेंस सूत्र
3	$f=R/2$	फोकस दूरी और वक्रता त्रिज्या
4	$m=h'/h=-v/u$	दर्पण में आवर्धन
5	$m=v/u$	लेंस में आवर्धन
6	$n=c/v$	अपवर्तनांक
7	$P=1/f$	लेंस की क्षमता (डाइऑप्टर)

✦ अत्यंत महत्वपूर्ण प्रश्नोत्तर (CBSE Repeated Q&A)

दर्पण सूत्र लिखकर किसी उदाहरण पर हल कीजिए।
अवतल दर्पण द्वारा बनने वाली प्रतिच्छवियों का आरेख सहित वर्णन कीजिए।
स्नेल का नियम (Snell’s Law) लिखकर उदाहरण दीजिए।
आवर्धन का सूत्र लिखिए और प्रतिबिंब की प्रकृति बताइए।
उत्तल दर्पण को वाहन के साइड मिरर में क्यों लगाया जाता है?
अपवर्तन के नियम लिखिए।
अपवर्तन से जुड़े दैनिक जीवन के उदाहरण बताइए।
उत्तल और अवतल लेंस के उपयोग लिखिए।
अपवर्तनांक की परिभाषा और सूत्र लिखिए।
लेंस की क्षमता (Power) समझाइए।

यह अध्याय प्रकाश की दो मूलभूत परिघटनाओं, परावर्तन (Reflection) और अपवर्तन (Refraction), की व्याख्या करता है। इसमें गोलीय दर्पणों और लेंसों द्वारा प्रतिबिंब बनने के नियम, सूत्र और उनके दैनिक जीवन में उपयोग शामिल हैं।

मुख्य विचार: प्रकाश सरल रेखा में चलता है। जब यह किसी चमकदार सतह से टकराता है तो परावर्तित होता है और जब एक माध्यम से दूसरे माध्यम में जाता है तो अपना पथ मोड़ लेता है, जिसे अपवर्तन कहते हैं।

विस्तृत नोट्स (Detailed Notes)

1. प्रकाश का परावर्तन (Reflection of Light)

परावर्तन के नियम:
1. आपतन कोण (∠i) सदैव परावर्तन कोण (∠r) के बराबर होता है। (∠i = ∠r)
2. आपतित किरण, आपतन बिंदु पर अभिलंब और परावर्तित किरण सभी एक ही तल में होते हैं।
समतल दर्पण:
- प्रतिबिंब आभासी, सीधा और बिंब के आकार के बराबर बनता है।
- प्रतिबिंब दर्पण के पीछे उतनी ही दूरी पर बनता है, जितनी दूरी पर दर्पण के सामने बिंब होता है।
- प्रतिबिंब पार्श्विक रूप से उलटा (laterally inverted) होता है।

2. गोलीय दर्पण (Spherical Mirrors)

प्रकार:
- अवतल दर्पण (Concave Mirror): परावर्तक सतह अंदर की ओर वक्रित होती है।
- उत्तल दर्पण (Convex Mirror): परावर्तक सतह बाहर की ओर वक्रित होती है।
मुख्य पद (Important Terms):
- ध्रुव (Pole – P): दर्पण के परावर्तक सतह का केंद्रीय बिंदु।
- वक्रता केंद्र (Centre of Curvature – C): उस गोले का केंद्र जिसका दर्पण एक भाग है।
- वक्रता त्रिज्या (Radius of Curvature – R): ध्रुव से वक्रता केंद्र तक की दूरी।
- मुख्य फोकस (Principal Focus – F): मुख्य अक्ष के समांतर किरणें परावर्तन के बाद जिस बिंदु पर मिलती हैं या जिस बिंदु से आती हुई प्रतीत होती हैं।
- फोकस दूरी (Focal Length – f): ध्रुव और मुख्य फोकस के बीच की दूरी।
- संबंध: $f=R/2f = R/2$
दर्पण सूत्र (Mirror Formula):
$1v+1u=1f\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
- जहाँ u = बिंब दूरी, v = प्रतिबिंब दूरी, f = फोकस दूरी
- चिह्न परिपाटी: दर्पण के सामने की दूरी ऋणात्मक और पीछे की दूरी धनात्मक ली जाती है।
आवर्धन (Magnification – m):
$m=h'/h=-v/u$
- h' = प्रतिबिंब की ऊँचाई, h = वस्तु की ऊँचाई
- $m>0m > 0$ : आभासी व सीधा प्रतिबिंब
- $m<0m < 0$ : वास्तविक व उल्टा प्रतिबिंब
उपयोग:
- अवतल दर्पण: टॉर्च, हेडलाइट, शेविंग मिरर, दंत चिकित्सक का दर्पण
- उत्तल दर्पण: वाहन का साइड/रियर-व्यू मिरर, सुरक्षा दर्पण

3. प्रकाश का अपवर्तन (Refraction of Light)

परिभाषा: एक माध्यम से दूसरे माध्यम में जाने पर प्रकाश का पथ मुड़ जाता है।
कारण: विभिन्न माध्यमों में प्रकाश की चाल अलग-अलग होती है।
अपवर्तन के नियम:
1. आपतित किरण, अपवर्तित किरण और अभिलंब एक ही तल में होते हैं।
2. स्नेल का नियम:
  $sin⁡isin⁡r=μ\frac{\sin i}{\sin r} = \mu$

4. अपवर्तनांक (Refractive Index)

परिभाषा:
$n=c/v$
जहाँ c = निर्वात में प्रकाश की चाल, v = माध्यम में प्रकाश की चाल
निरपेक्ष अपवर्तनांक ≥ 1 होता है।
प्रकाशिक घनत्व: अधिक अपवर्तनांक वाला माध्यम अधिक सघन होता है।

5. लेंस (Lenses)

प्रकार:
- उत्तल लेंस (Convex Lens): बीच से मोटा, किरणों को अभिसरित करता है।
- अवतल लेंस (Concave Lens): बीच से पतला, किरणों को अपसरित करता है।
लेंस सूत्र (Lens Formula):
$1/v-1/u=1/f$
आवर्धन (Magnification):
$m=h'/h=v/u$
लेंस की क्षमता (Power):
$P=1/f(f मीटर में)$
- मात्रक = डाइऑप्टर (D)
- उत्तल लेंस: +ve D
- अवतल लेंस: -ve D

CBSE परीक्षा के लिए महत्वपूर्ण बिंदु

चिह्न परिपाटी पर विशेष ध्यान दें।
दर्पण सूत्र और लेंस सूत्र के बीच अंतर याद रखें।
आवर्धन के सूत्र से प्रतिबिंब की प्रकृति तय करना सीखें।
f = R/2 याद रखें।
दैनिक जीवन के उपयोग से प्रश्न जरूर पूछे जाते हैं।
अपवर्तनांक का सूत्र $n=c/vn = c/v$ और प्रकाशिक घनत्व का संबंध याद रखें।
लेंस की क्षमता (P = 1/f) और डाइऑप्टर का ज्ञान जरूरी है।
किरण आरेख बनाने का अभ्यास करें।

सूत्रों की सारणी (Formula Sheet)

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

सभी प्रश्न और उत्तर (हिंदी में)

प्रश्न 1. उस उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए, जिसकी वक्रता–त्रिज्या 32 सेमी है।

उत्तर:
फोकस दूरी $f=R2f = \frac{R}{2}$
= $322\frac{32}{2}$ = 16 सेमी।

प्रश्न 2. कोई अवतल दर्पण आमने-सामने 10 सेमी की दूरी पर रखे किसी बिंदु का तीन गुना आवर्धित (बड़ा) वास्तविक प्रतिच्छवि बनाता है। प्रतिच्छवि दर्पण से कितनी दूरी पर है?

उत्तर:
वस्तु दूरी (u) = –10 सेमी, आवर्धन (M) = –3 (वास्तविक के लिए ऋणात्मक)
$M=v/u$
⇒ v = M × u = –3 × –10 = 30 सेमी।
अतः प्रतिच्छवि दर्पण से 30 सेमी दूरी पर है।

प्रश्न 3. वास्तविक जीवन में उत्तल दर्पण का प्रयोग कहाँ किया जाता है?

उत्तर:
उत्तल दर्पण का प्रयोग वाहनों में पार्श्वदर्पण (side mirror) के रूप में किया जाता है क्योंकि यह सीधा, छोटा और विस्तृत क्षेत्र दिखाने वाली प्रतिच्छवि बनाता है।

प्रश्न 4. जब प्रकाश किरण वायु से जल में प्रवेश करती है तो वह किस ओर झुकेगी? क्यों?

उत्तर:
प्रकाश जब वायु (कम सघन) से जल (अधिक सघन) में प्रवेश करता है तो वह अपभिलंब (normal) की ओर झुकती है, क्योंकि अधिक सघन माध्यम में प्रकाश की चाल कम हो जाती है।

प्रश्न 5. यदि काँच का अपवर्तनांक 1.5 है और प्रकाश की चाल निर्वात में 3 × 10⁸ m/s है तो काँच में प्रकाश की चाल क्या होगी?

प्रश्न 6. सारणी 9.3 से अधिकतम तथा न्यूनतम प्रकाशिक घनत्व वाले माध्यम बताइए।

उत्तर:

अधिकतम घनत्व: हीरा
न्यूनतम घनत्व: वायु

प्रश्न 7. हीरे का अपवर्तनांक 2.42 है। इस कथन का क्या अर्थ है?

उत्तर:
इसका अर्थ है कि निर्वात में प्रकाश की चाल हीरे में उसकी चाल से 2.42 गुना अधिक है।

✦ पिछले वर्षों के CBSE परीक्षा से महत्वपूर्ण प्रश्न

प्रश्न: उत्तल दर्पण को वाहन के रियर-व्यू मिरर (rear-view mirror) के रूप में क्यों प्रयोग किया जाता है?
उत्तर: क्योंकि यह सीधा, छोटा और विस्तृत क्षेत्र की प्रतिच्छवि बनाता है, जिससे चालक सड़क का बड़ा हिस्सा देख सकता है।
प्रश्न: अवतल दर्पण का उपयोग दंत चिकित्सक (dentist) क्यों करते हैं?
उत्तर: क्योंकि अवतल दर्पण वस्तु को बड़ा और सीधा दिखाता है, जिससे दाँत को आसानी से देखा जा सकता है।
प्रश्न: 20 सेमी फोकस दूरी वाले अवतल दर्पण से बनी प्रतिच्छवि वस्तु की दोगुनी है। वस्तु की स्थिति ज्ञात कीजिए।
उत्तर: सूत्र $1f=1v+1u\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$ का उपयोग कर हल किया जाता है।
प्रश्न: अपवर्तनांक का परिभाषा लिखिए और इसका सूत्र दीजिए।
उत्तर: किसी माध्यम का अपवर्तनांक (μ) = निर्वात में प्रकाश की चाल (c) ÷ उस माध्यम में प्रकाश की चाल (v)।

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

🔹 महत्वपूर्ण प्रश्न–उत्तर (Short + Long)

🟢 लघु उत्तरीय प्रश्न (Short Answer Questions)

प्रश्न 1. दर्पण सूत्र लिखिए और उसमें प्रयुक्त चिन्हों का अर्थ बताइए।
उत्तर:
दर्पण सूत्र –

$1/f=1/v+1/u$

जहाँ –

$f$ = दर्पण की फोकस दूरी
$v$ = प्रतिच्छवि की दूरी
$u$ = वस्तु की दूरी

प्रश्न 2. आवर्धन (Magnification) क्या है? इसका सूत्र लिखिए।
उत्तर:

परिभाषा:
आवर्धन (Magnification, $M$ ) किसी दर्पण या लेंस द्वारा बनी प्रतिच्छवि की ऊँचाई (h′) और वस्तु की ऊँचाई (h) के अनुपात को कहते हैं।

सूत्र:

जहाँ,

$h^{'} =$ प्रतिच्छवि की ऊँचाई (Height of Image)
$h =$ वस्तु की ऊँचाई (Height of Object)
$v =$ प्रतिच्छवि की दूरी (Image Distance)

ऋणात्मक आवर्धन ⇒ प्रतिच्छवि वास्तविक एवं उलटी

प्रश्न 3. अवतल दर्पण के दो उपयोग लिखिए।
उत्तर:

वाहन की हेडलाइट में समानांतर किरणों का प्रवाह करने हेतु।
दंत चिकित्सक तथा शेविंग मिरर में बड़ी प्रतिच्छवि देखने हेतु।

प्रश्न 4. अपवर्तनांक का परिभाषा लिखिए।
उत्तर:
किसी माध्यम का अपवर्तनांक = निर्वात में प्रकाश की चाल ÷ उस माध्यम में प्रकाश की चाल।

$μ=cv\mu = \frac{c}{v}$

प्रश्न 5. जब प्रकाश वायु से काँच में प्रवेश करता है तो किस ओर झुकता है और क्यों?
उत्तर:
प्रकाश अपभिलंब की ओर झुकता है, क्योंकि काँच वायु से अधिक सघन माध्यम है और उसमें प्रकाश की चाल कम हो जाती है।

प्रश्न 6. उत्तल दर्पण को वाहनों में रियर-व्यू मिरर के रूप में क्यों प्रयोग किया जाता है?
उत्तर:
क्योंकि यह छोटा, सीधा और विस्तृत क्षेत्र दिखाने वाली प्रतिच्छवि बनाता है।

🟢 दीर्घ उत्तरीय प्रश्न (Long Answer Questions)

प्रश्न 7. अवतल दर्पण द्वारा बनने वाली प्रतिच्छवियों का वर्णन कीजिए।
उत्तर:
अवतल दर्पण वस्तु की स्थिति पर निर्भर करते हुए अलग–अलग प्रकार की प्रतिच्छवि बनाता है –

अनंत पर वस्तु ⇒ अत्यधिक छोटी, वास्तविक, उलटी
C से परे ⇒ छोटी, वास्तविक, उलटी
C पर ⇒ समान आकार की, वास्तविक, उलटी
C और F के बीच ⇒ बड़ी, वास्तविक, उलटी
F पर ⇒ प्रतिच्छवि नहीं बनती
F और P के बीच ⇒ बड़ी, आभासी, सीधी

प्रश्न 8. उत्तल दर्पण की विशेषताएँ और उसके उपयोग लिखिए।
उत्तर:

यह सदैव छोटी, आभासी और सीधी प्रतिच्छवि बनाता है।
उपयोग :
1. वाहन के साइड मिरर के रूप में
2. सुरक्षा निगरानी (CCTV) में
3. दुकानों/मॉल में निगरानी हेतु

प्रश्न 9. स्नेल का नियम (Snell’s Law) लिखिए।
उत्तर:
अपवर्तन के नियम –

आपतन किरण, अपवर्तित किरण और अभिलंब एक ही तल में होते हैं।
आपतन कोण और अपवर्तन कोण के sine का अनुपात एक नियतांक होता है।

$sin⁡isin⁡r=μ\frac{\sin i}{\sin r} = \mu$

प्रश्न 10. अपवर्तन के दैनिक जीवन में चार उदाहरण दीजिए।
उत्तर:

जल में डूबी पेंसिल टेढ़ी दिखाई देती है।
काँच के स्लैब पर रखे अक्षर ऊपर उठे हुए दिखाई देते हैं।
तालाब की गहराई वास्तविक से कम प्रतीत होती है।
इंद्रधनुष का निर्माण।

प्रश्न 11. दर्पण सूत्र को स्पष्ट कीजिए। (लंबा प्रश्न)
उत्तर (संक्षेप में):
गोलीय दर्पणों के लिए वस्तु दूरी (u), प्रतिच्छवि दूरी (v) और फोकस दूरी (f) के बीच संबंध –

$1f=1v+1u\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$

यह सूत्र दोनों प्रकार के दर्पणों (अवतल और उत्तल) पर लागू होता है।

प्रश्न 12. अवतल दर्पण और उत्तल दर्पण के बीच अंतर लिखिए।
उत्तर:

बिंदु	अवतल दर्पण	उत्तल दर्पण
परावर्तक सतह	भीतर की ओर	बाहर की ओर
प्रतिच्छवि	वास्तविक/आभासी दोनों	सदैव आभासी
उपयोग	हेडलाइट, शेविंग मिरर	साइड मिरर, सुरक्षा दर्पण

🟢 अत्यंत महत्वपूर्ण प्रश्न (CBSE बोर्ड में बार-बार पूछे गए)

दर्पण सूत्र लिखकर किसी प्रश्न का हल कीजिए।
अवतल दर्पण द्वारा बनने वाली प्रतिच्छवियों का आरेख सहित वर्णन कीजिए।
स्नेल का नियम उदाहरण सहित समझाइए।
आवर्धन (Magnification) का सूत्र निकालिए।
वाहन में उत्तल दर्पण का उपयोग क्यों किया जाता है?
अपवर्तन के नियम लिखिए।
दैनिक जीवन में अपवर्तन से संबंधित उदाहरण दीजिए।
किसी वस्तु को अवतल दर्पण से उसकी फोकस दूरी से बाहर रखने पर बनने वाली प्रतिच्छवि का प्रकार बताइए।
उत्तल दर्पण सदैव आभासी और सीधी प्रतिच्छवि क्यों बनाता है?
अपवर्तनांक की परिभाषा और उसका गणितीय सूत्र दीजिए।

👉

बहुत अच्छा ✅
अब मैं आपके लिए अत्यंत महत्वपूर्ण प्रश्नों (जो CBSE बोर्ड में बार-बार पूछे गए हैं) के आसान और परीक्षा-उपयोगी उत्तर लिख रहा हूँ।

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

🔥 अत्यंत महत्वपूर्ण प्रश्नोत्तर (CBSE Board Repeated)

प्रश्न 1. दर्पण सूत्र लिखकर किसी प्रश्न का हल कीजिए।

उत्तर:
दर्पण सूत्र –

$1f=1v+1u\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$

जहाँ,

$ff$ = फोकस दूरी
$uu$ = वस्तु दूरी
$vv$ = प्रतिच्छवि दूरी

उदाहरण:
एक अवतल दर्पण की फोकस दूरी 20 सेमी है। 30 सेमी दूरी पर रखी वस्तु की प्रतिच्छवि कहाँ बनेगी?

$1f=1v+1u\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$ $120=1v+1−30\frac{1}{20} = \frac{1}{v} + \frac{1}{-30}$ $1v=120+130=560\frac{1}{v} = \frac{1}{20} + \frac{1}{30} = \frac{5}{60}$

⇒ $v=12 सेमीv = 12 \, \text{सेमी}$
प्रतिच्छवि वास्तविक, उलटी और दर्पण से 12 सेमी पर बनेगी।

प्रश्न 2. अवतल दर्पण द्वारा बनने वाली प्रतिच्छवियों का आरेख सहित वर्णन कीजिए।

उत्तर:
अवतल दर्पण में वस्तु की स्थिति के अनुसार प्रतिच्छवि –

अनंत पर ⇒ बिंदु आकार की, वास्तविक व उलटी
C से बाहर ⇒ छोटी, वास्तविक व उलटी
C पर ⇒ समान आकार की, वास्तविक व उलटी
C और F के बीच ⇒ बड़ी, वास्तविक व उलटी
F पर ⇒ प्रतिच्छवि नहीं बनती
F और P के बीच ⇒ बड़ी, आभासी व सीधी

(परीक्षा में आरेख अनिवार्य है – वस्तु, दर्पण, किरणें और प्रतिच्छवि दिखानी होती है।)

प्रश्न 3. स्नेल का नियम (Snell’s Law) उदाहरण सहित समझाइए।

उत्तर:
अपवर्तन के नियम:

आपतन किरण, अपवर्तित किरण और अभिलंब एक ही तल में होते हैं।

\frac{\sin i}{\sin r} = \mu
]
जहाँ, $ii$ = आपतन कोण, $rr$ = अपवर्तन कोण, $μ\mu$ = अपवर्तनांक

उदाहरण: जब प्रकाश वायु (कम सघन) से जल (अधिक सघन) में जाता है तो किरण अभिलंब की ओर झुकती है।

प्रश्न 4. आवर्धन (Magnification) का सूत्र निकालिए।

उत्तर:

$M=प्रतिच्छवि की ऊँचाई (h’)वस्तु की ऊँचाई (h)=h′hM = \frac{\text{प्रतिच्छवि की ऊँचाई (h’)}}{\text{वस्तु की ऊँचाई (h)}} = \frac{h’}{h}$

इसके अतिरिक्त,

$M=vuM = \frac{v}{u}$

यदि $MM$ धनात्मक है ⇒ प्रतिच्छवि आभासी व सीधी
यदि $MM$ ऋणात्मक है ⇒ प्रतिच्छवि वास्तविक व उलटी

प्रश्न 5. वाहन में उत्तल दर्पण का उपयोग क्यों किया जाता है?

उत्तर:

यह सदैव सीधी और आभासी प्रतिच्छवि बनाता है।
यह प्रतिच्छवि वस्तु से छोटी होती है, जिससे बड़ा क्षेत्र दिखाई देता है।
चालक सड़क का अधिक भाग देख पाता है, जिससे सुरक्षा बढ़ती है।

प्रश्न 6. अपवर्तन के नियम लिखिए।

उत्तर:

अपवर्तन के नियम (Laws of Refraction):

पहला नियम:
आपतन किरण, अपवर्तित किरण और आपतन बिंदु पर खींचा गया अभिलंब — ये तीनों एक ही तल (Plane) में होते हैं।
दूसरा नियम (स्नेल का नियम – Snell’s Law):
किसी भी दो माध्यमों के लिए —
जहाँ,
- आपतन कोण (Angle of Incidence)
- अपवर्तन कोण (Angle of Refraction)
- $=$ दूसरे माध्यम का पहले माध्यम के सापेक्ष अपवर्तनांक (Refractive Index)

👉 निष्कर्ष:

यदि प्रकाश कम सघन से अधिक सघन माध्यम में जाता है ⇒ किरण अभिलंब की ओर झुकती है।
यदि प्रकाश अधिक सघन से कम सघन माध्यम में जाता है ⇒ किरण अभिलंब से हटकर झुकती है।

प्रश्न 7. दैनिक जीवन में अपवर्तन से संबंधित उदाहरण दीजिए।

उत्तर:

जल में डूबी पेंसिल टेढ़ी दिखाई देती है।
तालाब की गहराई वास्तविक से कम प्रतीत होती है।
काँच के स्लैब पर रखे अक्षर ऊपर उठे दिखते हैं।
पानी में पड़ा सिक्का ऊपर उठा हुआ लगता है।

प्रश्न 8. किसी वस्तु को अवतल दर्पण से उसकी फोकस दूरी से बाहर रखने पर बनने वाली प्रतिच्छवि का प्रकार बताइए।

उत्तर:

यदि वस्तु C और अनंत के बीच रखी हो ⇒ प्रतिच्छवि छोटी, वास्तविक, उलटी।
यदि वस्तु C और F के बीच रखी हो ⇒ प्रतिच्छवि बड़ी, वास्तविक, उलटी।

प्रश्न 9. उत्तल दर्पण सदैव आभासी और सीधी प्रतिच्छवि क्यों बनाता है?

उत्तर:
क्योंकि उत्तल दर्पण की परावर्तित किरणें सदैव अपसारी (diverging) होती हैं। ये किरणें पीछे की ओर बढ़ाने पर मिलती प्रतीत होती हैं, जिससे प्रतिच्छवि आभासी और सीधी बनती है।

प्रश्न 10. अपवर्तनांक की परिभाषा और उसका गणितीय सूत्र दीजिए।

उत्तर:
परिभाषा: किसी माध्यम का अपवर्तनांक उस माध्यम में प्रकाश की चाल की तुलना में निर्वात में प्रकाश की चाल का अनुपात होता है।
सूत्र:

$μ=c/v$

जहाँ,

$c$ = निर्वात में प्रकाश की चाल (3 × 10⁸ m/s)
$v$ = माध्यम में प्रकाश की चाल

📘 अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन (Light – Reflection and Refraction)

✦ पाठ का सारांश (Chapter Summary)

✦ विस्तृत नोट्स (Detailed Notes)

🔹 1. प्रकाश का परावर्तन (Reflection of Light)

🔹 2. गोलीय दर्पण (Spherical Mirrors)

चिह्न परिपाटी (Sign Convention for Mirrors)

🔹 3. प्रकाश का अपवर्तन (Refraction of Light)

अपवर्तन के नियम (Laws of Refraction / Snell’s Law)

🔹 4. अपवर्तनांक (Refractive Index)

🔹 5. लेंस (Lenses)

✦ CBSE परीक्षा के लिए महत्वपूर्ण बिंदु

✦ सूत्रों की सारणी (Formula Sheet)

✦ अत्यंत महत्वपूर्ण प्रश्नोत्तर (CBSE Repeated Q&A)

विस्तृत नोट्स (Detailed Notes)

1. प्रकाश का परावर्तन (Reflection of Light)

2. गोलीय दर्पण (Spherical Mirrors)

3. प्रकाश का अपवर्तन (Refraction of Light)

4. अपवर्तनांक (Refractive Index)

5. लेंस (Lenses)

CBSE परीक्षा के लिए महत्वपूर्ण बिंदु

सूत्रों की सारणी (Formula Sheet)

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

सभी प्रश्न और उत्तर (हिंदी में)

प्रश्न 1. उस उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए, जिसकी वक्रता–त्रिज्या 32 सेमी है।

प्रश्न 3. वास्तविक जीवन में उत्तल दर्पण का प्रयोग कहाँ किया जाता है?

प्रश्न 4. जब प्रकाश किरण वायु से जल में प्रवेश करती है तो वह किस ओर झुकेगी? क्यों?

प्रश्न 5. यदि काँच का अपवर्तनांक 1.5 है और प्रकाश की चाल निर्वात में 3 × 10⁸ m/s है तो काँच में प्रकाश की चाल क्या होगी?

प्रश्न 6. सारणी 9.3 से अधिकतम तथा न्यूनतम प्रकाशिक घनत्व वाले माध्यम बताइए।

प्रश्न 7. हीरे का अपवर्तनांक 2.42 है। इस कथन का क्या अर्थ है?

✦ पिछले वर्षों के CBSE परीक्षा से महत्वपूर्ण प्रश्न

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

🔹 महत्वपूर्ण प्रश्न–उत्तर (Short + Long)

🟢 लघु उत्तरीय प्रश्न (Short Answer Questions)

🟢 दीर्घ उत्तरीय प्रश्न (Long Answer Questions)

🟢 अत्यंत महत्वपूर्ण प्रश्न (CBSE बोर्ड में बार-बार पूछे गए)

✦ अध्याय 9 : प्रकाश – परावर्तन तथा अपवर्तन

🔥 अत्यंत महत्वपूर्ण प्रश्नोत्तर (CBSE Board Repeated)

प्रश्न 1. दर्पण सूत्र लिखकर किसी प्रश्न का हल कीजिए।

प्रश्न 2. अवतल दर्पण द्वारा बनने वाली प्रतिच्छवियों का आरेख सहित वर्णन कीजिए।

प्रश्न 3. स्नेल का नियम (Snell’s Law) उदाहरण सहित समझाइए।

प्रश्न 4. आवर्धन (Magnification) का सूत्र निकालिए।

प्रश्न 5. वाहन में उत्तल दर्पण का उपयोग क्यों किया जाता है?

प्रश्न 6. अपवर्तन के नियम लिखिए।

उत्तर:

प्रश्न 7. दैनिक जीवन में अपवर्तन से संबंधित उदाहरण दीजिए।

प्रश्न 8. किसी वस्तु को अवतल दर्पण से उसकी फोकस दूरी से बाहर रखने पर बनने वाली प्रतिच्छवि का प्रकार बताइए।

प्रश्न 9. उत्तल दर्पण सदैव आभासी और सीधी प्रतिच्छवि क्यों बनाता है?

प्रश्न 10. अपवर्तनांक की परिभाषा और उसका गणितीय सूत्र दीजिए।

Click here for More Notes for Xth CBSE Class – Click

Leave a comment Cancel reply